斐波那契详解:数列、黄金比例、种类与MT4/MT5绘制方法
斐波那契数列由义大利数学家「雷奥纳多·斐波那契」所发现,是一个经典的数学数列。
这个数列以「1、1、2、3、5、8、13…」的形式呈现,从1开始,每一个数字都是前两个数字相加的结果,这便是我们熟知的斐波那契数列。
斐波那契数列所衍生出的各种比率,已经在金融市场中广泛应用,并成为分析价格波动的有力工具。
本文将深入探讨斐波那契的基本概念、数列与比率、黄金比例,以及在MT4/MT5平台上的绘制方法等相关内容。
斐波那契解读:从斐波那契数列到斐波那契比率的解析
下文将深入解析斐波那契数列与斐波那契比率的运作原理。
斐波纳契数列
斐波那契数列是从1开始,将相邻的两个数字相加,产生下一个数字,并不断延伸形成数列。
1、1、2、3、5、8、13、21、34、55、89、144、233、377、610、987、1597、2584、4181、6765、10946…
例如,将最初的「1」与第二个「1」相加,第三个数字就是「2」。
同样的,将第二个「1」与第三个「2」相加,第四个数字是「3」,第三个「2」与第四个「3」相加,得到第五个数字「5」,依此类推。
这种规律性是斐波纳契数列的最大特色,可以转化为以下公式:
F(0) = 0,
F(1) = 1,
F(n) = F(n−1) + F(n−2) (n≥2)
斐波那契数列的起源
斐波那契数列以义大利数学家斐波那契(Fibonacci)的名字命名,斐波那契的本名是李奥纳多·皮萨诺(Leonardo of Pisa)。他生活在13世纪,是欧洲中世纪最著名的数学家之一。斐波那契在1202年出版的《算经》(Liber Abaci)一书中首次提出了这一数字。
斐波那契数列的发现源自于一个有趣的数学问题:假设一个理想条件下的兔子繁殖问题。在每个月,一对兔子会繁殖出一对新兔子,而新兔子在第二个月开始繁殖。起初有一对兔子,经过若干个月后会有多少对兔子?透过这个问题,斐波那契推导出了著名的斐波那契数列。
这一数列不仅在数学领域有着广泛的应用,在自然界中也能看到斐波那契数列的身影。例如,向日葵的种子排列、贝壳的螺旋形状、松果的鳞片分布等,都是斐波那契数列在自然界中的体现。
斐波纳契比率(黄金比例)
斐波纳契比率是从斐波纳契数列中导出的各种比率。
当我们注意到这些比率时,可以发现它们遵循着一定的法则(接近下表中的数值)。
透过改变分割的方式,我们可以得到各种不同的比率。
以下是一些主要的斐波纳契比率:
| 斐波那契比率 | 计算方法 |
| 0.236(23.6%) | 任意数字除以该数字后间隔两个位置的数字(例如:55 ÷ 233 = 0.236) |
| 0.382(38.2%) | 任意数字除以该数字后间隔一个位置的数字(例如:34 ÷ 89 = 0.382) |
| 0.618(61.8%) | 任意数字除以其后紧邻的数字(例如:144 ÷ 233 = 0.618) |
| 1.618(161.8%) | 任意数字除以其前紧邻的数字(例如:610 ÷ 377 = 1.618) |
| 2.618(261.8%) | 任意数字除以该数字前间隔一个位置的数字(例如:987 ÷ 377 = 2.618) |
| 4.236(423.6%) | 任意数字除以该数字前间隔两个位置的数字(例如:1597 ÷ 377 = 4.236) |
其中,1.618(161.8%)是所谓的黄金比例,这个比例被认为是世界上最美的平衡比例,「1对1.618」被认为是最具美感的比例。
黄金比例的定义
黄金比例是指将一条线段分为两部分时,较长部分(a)与较短部分(b)的比例等于整个线段(a + b)与较长部分(a)的比例,即:
⌀= (a+b) / a = a/b,
其中,⌀ ≈ 1.6180339887…
黄金比已经被广泛应用于建筑、艺术作品,甚至名片等日常物品。
这些斐波纳契比率经过多年的研究,已经被发展出许多可以在技术分析中使用的工具。
斐波那契工具的种类(MT4 & MT5)
由于「斐波那契(Fibonacci)」一词来自英文翻译,因此在MetaTrader 4(MT4)和MetaTrader 5(MT5)平台上,斐波那契工具的中文名称存在一些细微的差别。
以下是这些工具的英文名称及其在MT4和MT5平台上的中文翻译,其中斐波那契回调线是最常用的工具之一:
| 英文名称 (English) | MT4中文名称 | MT5中文名称 | 说明 |
| Fibonacci Retracement | 斐波纳奇回调线 | 斐波纳契回调线 | 用于识别价格回调时的潜在支撑和阻力等级。 |
| Fibonacci Time Zones | 斐波纳奇时间区间 | 斐波纳契时间周期线 | 透过时间轴上的斐波那契比率划分,用于预测趋势变化的时间点。 |
| Fibonacci Fan | 斐波纳奇扇形线 | 斐波纳契角度线 | 基于斐波那契比率从一个起点向多个方向延伸,用于确定支撑和阻力线。 |
| Fibonacci Arcs | 斐波纳奇弧线 | 斐波纳契扇形线 | 利用斐波那契比率在价格和时间轴上绘制弧线,用于识别潜在的支撑和阻力水平。 |
| Fibonacci Expansion | 斐波纳奇扩展线 | 斐波纳契扩展 | 用于预测趋势方向中的新价格目标,常用于设定获利目标。 |
| Fibonacci Channel | - | 斐波纳契通道 | 建立平行通道线,用于确定突破点和趋势变化。 |
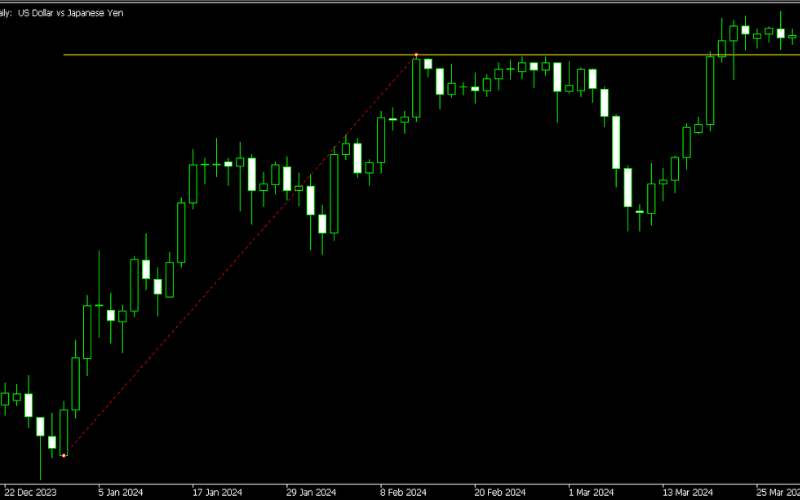
斐波那契回调线 (Fibonacci Retracement)
斐波那契回调线(Fibonacci Retracement)是技术分析中常用的工具,旨在识别市场价格回调时的潜在支撑和阻力水平。
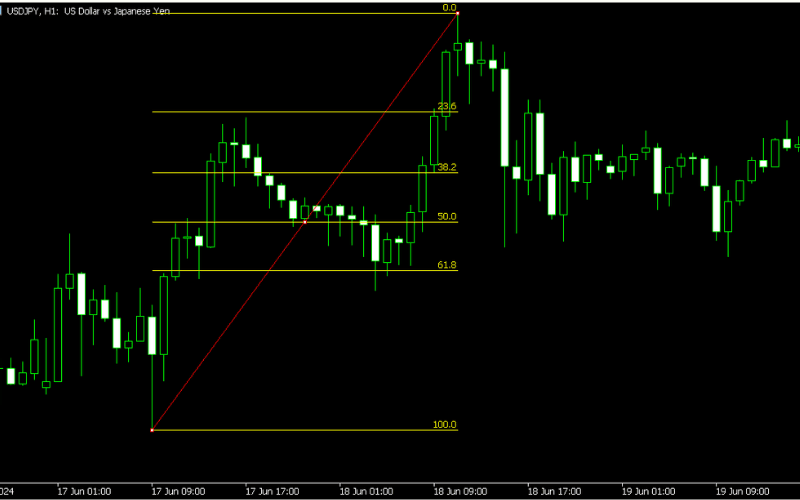
该工具基于斐波那契数列,透过在价格趋势的起点和终点之间绘制一系列水平线,帮助交易者预测价格可能回调的关键区域。
斐波纳契回调幅度计算方法
计算公式:C(X%) = B − ( B − A ) × X%
•A 是起点价格(低点或高点)
•B 是终点价格(高点或低点)
•X% 是斐波那契回调比例(如 23.6%、38.2%、50%、61.8% 等)
•C(X%) 是对应的回调位价格
这个公式的意思是:从终点价格 B 开始,回调价格范围 (B - A) 的 X%,得到回调幅度 C(X%)。

这些幅度代表价格回调的百分比,即价格从高点回调到低点的比例。每个回调幅度都有其重要的意义。
| 回调幅度 | 计算公式 | 说明 |
| 23.6% 回调 | C(23.6%) = B − (B − A) × 0.236 | 上升趋势中较弱的回调;在下降趋势中为较弱反弹。 |
| 38.2% 回调 | C(38.2%) = B − (B − A) × 0.382 | 上升趋势中常见的回调支撑位;在下降趋势中为常见反弹阻力位。 |
| 50% 回调 | C(50%) = B − (B − A) × 0.5 | 一个心理关卡,广泛用于技术分析;在上升和下降趋势中都常见。 |
| 61.8% 回调 | C(61.8%) = B − (B − A) × 0.618 | 上升趋势中的黄金回调支撑位;在下降趋势中为黄金反弹阻力位。 |
| 78.6% 回调 | C(78.6%) = B − (B − A) × 0.786 | 上升趋势中较深的回调,可能表示趋势反转;在下降趋势中为较深反弹,可能表示趋势反转。 |
斐波那契时间周期线 (Fibonacci Time Zones)
斐波那契时间周期线是技术分析中的一种独特工具,专注于时间轴上的斐波那契比率划分,帮助交易者预测趋势变化的关键时间点。
该工具适合用于识别趋势反转或加速的时间窗口,为交易者提供时间维度的参考。
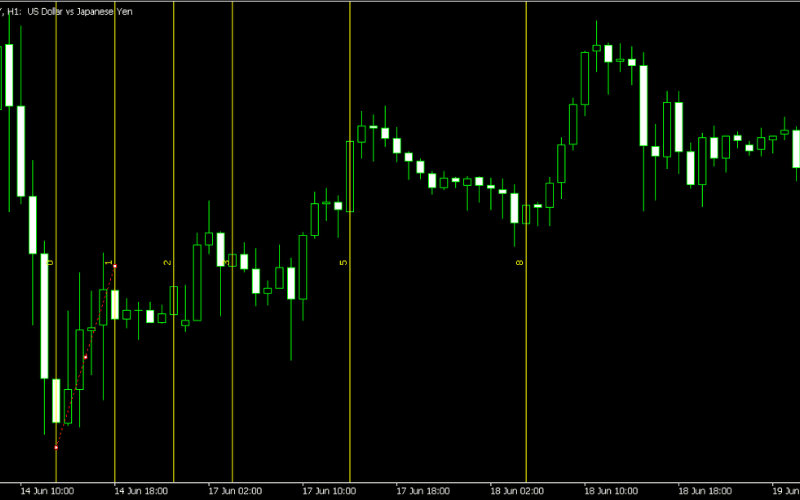
斐波那契角度线 (Fibonacci Fan)
斐波那契角度线是一种结合价格与时间的技术分析工具,透过从趋势起点向多个方向绘制斐波那契比率线,帮助交易者识别潜在的支撑和阻力区域。
该工具用于预测价格回调或反弹的关键区域,特别适合趋势追踪交易。
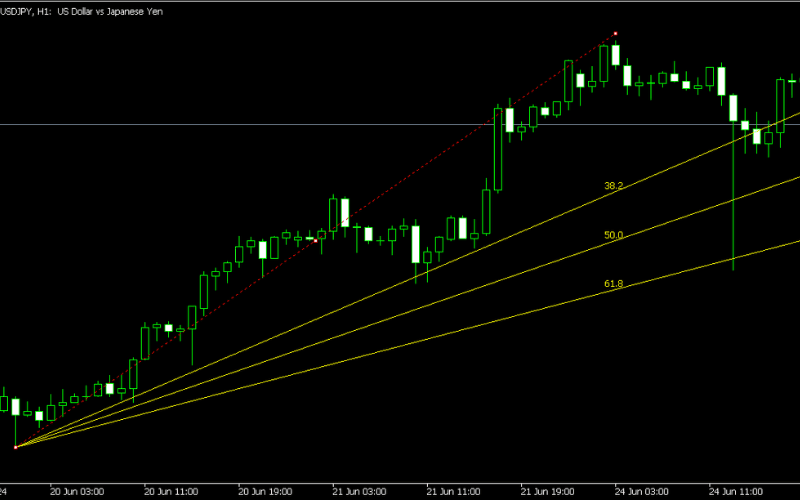
斐波那契扇形线 (Fibonacci Arcs)
斐波那契扇形线是一种结合价格与时间的弧形分析工具,透过在趋势起点和终点之间绘制弧形斐波那契比率线,标示出潜在的市场变化区域。
该工具适合用于识别价格回调或突破的关键区域,尤其在震荡市场中表现出色。
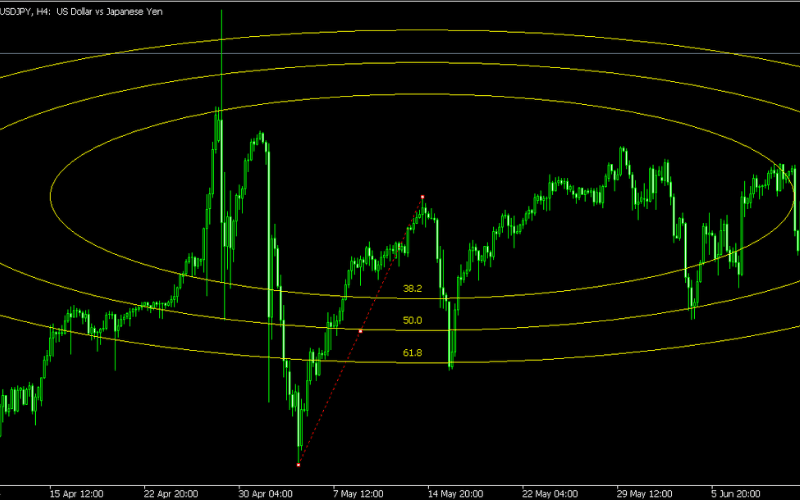
斐波那契扩展 (Fibonacci Expansion)
斐波那契扩展是一种用于预测价格趋势延伸目标的工具,帮助交易者设定获利目标或识别潜在的反转点。
该工具常用于趋势追踪交易,为交易者提供明确的获利了结或加仓参考。
斐波那契通道 (Fibonacci Channel)
斐波那契通道是一种结合趋势线与斐波那契比率的技术分析工具,透过创建平行通道线,帮助交易者识别趋势变化和突破点。
该工具适合用于预测价格在通道内的波动范围,并识别突破或反转的信号。

斐波那契工具的绘制方法(MT4/MT5)
在MetaTrader 4(MT4)和MetaTrader 5(MT5)平台上绘制斐波那契工具时,虽然基本步骤相似,但介面和某些细节操作上有些许区别。以下将分别介绍如何在MT4和MT5平台上绘制斐波那契工具。
MT4中绘制斐波那契工具的方法
MT4提供5种斐波那契工具。
①登入MT4
②打开交易品种的图表
③点选选单栏的「插入」-「斐波纳奇」,然后选择1个斐波那契的工具。
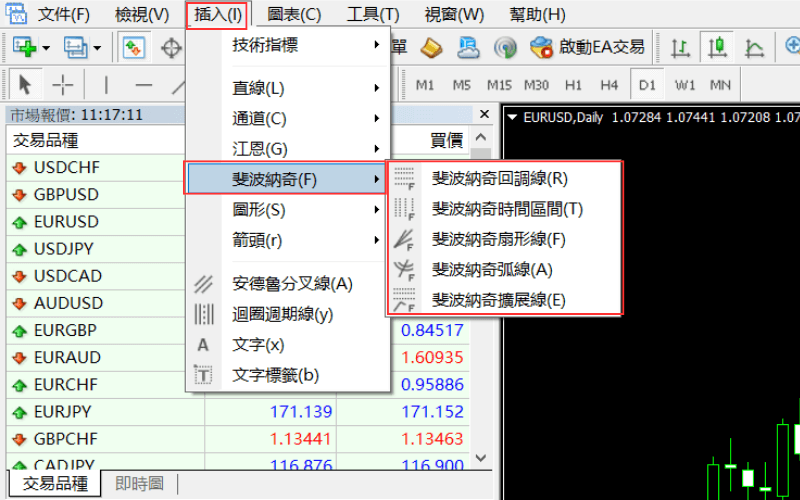
斐波那契工具的绘制方法(MT4/MT5)
MT5提供6种斐波那契工具。
①登入MT5
②打开交易品种的图表
③点选选单栏的「插入」-「对象」-「斐波那契」,然后选择1个斐波那契的工具。
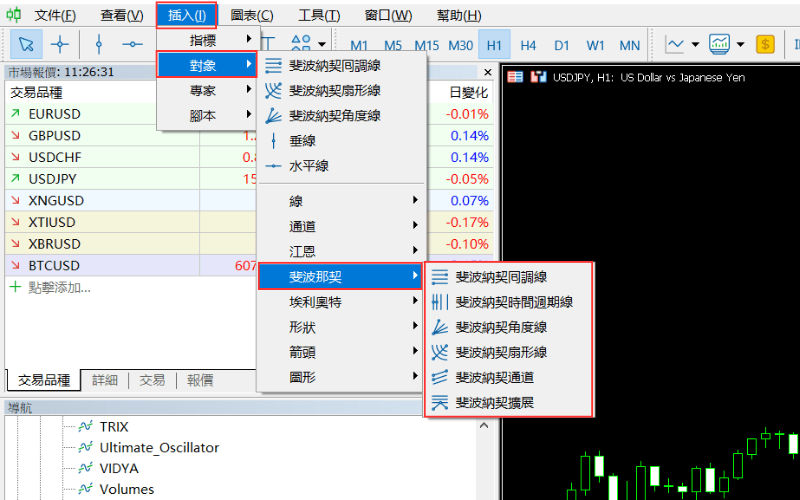
斐波纳契相关Q&A
Q1:斐波纳契与枢轴点有何区别?
斐波纳契工具(如回撤与扩展等)与枢轴点的区别在于计算的基础。
斐波纳契是基于特定波动,使用斐波纳契数列中的黄金比进行计算,并显示出回撤、反弹或延伸的目标。
而枢轴点则是根据前一交易日的「K线数据」来计算,并显示出可能的支撑与压力位。
Q2:斐波纳契的「兔子问题」的答案是什么?
「兔子问题」出自斐波纳契的著作《Liber Abaci》中的一个数学问题,问题内容为:
若一对兔子从出生两个月后每月繁殖一对兔子,则一年后兔子的数量会是多少?
0到1个月后会有一对,2个月后会有两对,3个月后会有三对,4个月后会有五对,以此类推,和斐波那契数列一样:1,1,2,3,5,8,13,21,34,55,89,144,233......12个月后会有233对。
这个问题的答案透过斐波纳契数列的规则来解,最终一年后将有233对兔子。
总结
斐波那契数列由义大利数学家李奥纳多·斐波那契于13世纪提出,源自于兔子繁殖问题,其数列(1, 1, 2, 3, 5, 8...)及其衍生的黄金比例(61.8%、38.2%等)在金融市场中广泛应用。
斐波那契回撤工具帮助交易者识别价格回调的支撑与阻力位,而斐波那契扩展则用于预测趋势延续的目标位,两者结合技术分析可提升交易策略的准确性。
虽然斐波那契工具简单直观且适用范围广,但其主观性与历史数据的局限性需谨慎对待,建议结合其他指标(如移动平均线、RSI)及风险管理措施,并善用MT4/MT5平台的自动化工具,以在市场中更稳健地捕捉机会。

